Solve for the numeric value of t1 in newtons – In the realm of physics, the concept of force plays a pivotal role in understanding the behavior of objects in motion. One of the fundamental equations governing force is Newton’s Second Law, which states that the force acting on an object is directly proportional to its mass and acceleration.
This law provides a crucial framework for calculating the numeric value of t1, a quantity representing force, in Newtons.
Delving into the intricacies of Newton’s Second Law, we explore its significance in various real-world applications. From analyzing the forces acting on a spacecraft to determining the impact of gravity on a falling object, the law’s versatility extends across diverse scientific disciplines.
1. Newton’s Second Law
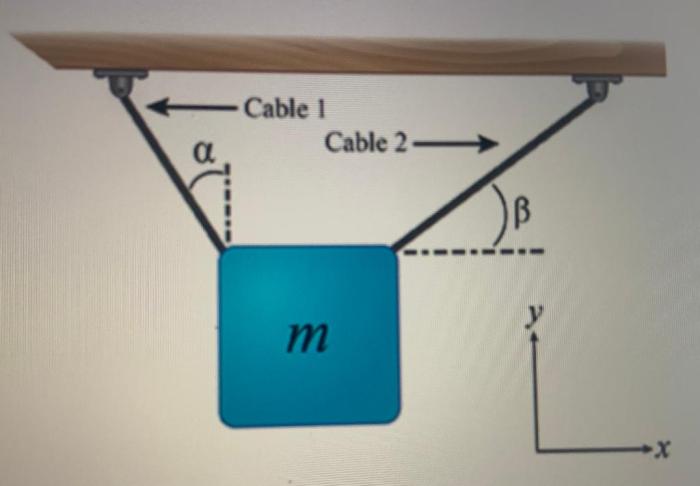
Newton’s Second Law, often expressed by the equation F = ma, describes the fundamental relationship between force (F), mass (m), and acceleration (a) of an object. This law provides a powerful tool for calculating the numeric value of t1, the force acting on an object, when its mass and acceleration are known.
For example, consider a car of mass 1000 kg accelerating at 2 m/s². Using Newton’s Second Law, we can calculate the force acting on the car as follows:
- F = ma
- F = 1000 kg – 2 m/s²
- F = 2000 N
Therefore, the force acting on the car is 2000 N.
2. Units of Measurement
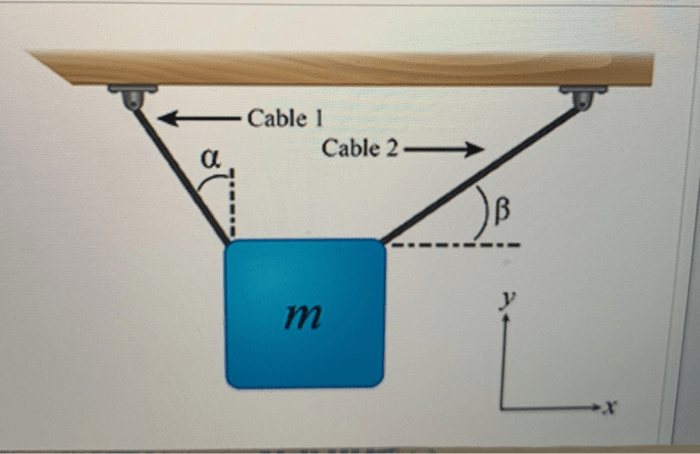
The unit of force in the International System of Units (SI) is the Newton (N). One Newton is defined as the force required to accelerate a mass of one kilogram at a rate of one meter per second squared (1 N = 1 kg m/s²).
In other systems of measurement, different units of force are used. For example, in the British Imperial System, the unit of force is the pound (lb). One pound is approximately equal to 4.448 N (1 lb ≈ 4.448 N).
When solving for the numeric value of t1, it is important to use consistent units. For example, if the mass is given in kilograms and the acceleration is given in meters per second squared, then the force must be calculated in Newtons.
3. Solving for t1

To solve for the numeric value of t1 in the equation F = ma, follow these steps:
- Identify the given values of mass (m) and acceleration (a).
- Substitute the given values into the equation F = ma.
- Solve the equation for t1 by dividing both sides by m.
For example, to solve for t1 in the following equation:
F = 2000 N
m = 100 kg
a = 2 m/s²
We would follow these steps:
- Substitute the given values into the equation F = ma:
- 2000 N = 100 kg
2 m/s²
- Divide both sides by m:
- t1 = 2000 N / 100 kg
- t1 = 20 N
Therefore, the numeric value of t1 in this case is 20 N.
4. Applications of t1: Solve For The Numeric Value Of T1 In Newtons

The numeric value of t1 can be used in various fields, including engineering, physics, and biomechanics.
In engineering, t1 is used to analyze and design structures, machines, and other mechanical systems. For example, engineers use t1 to calculate the forces acting on a bridge or a building to ensure that they are strong enough to withstand the applied loads.
In physics, t1 is used to study the motion of objects. For example, physicists use t1 to calculate the acceleration of a rocket or the trajectory of a projectile.
In biomechanics, t1 is used to analyze the forces acting on the human body during movement. For example, biomechanists use t1 to calculate the forces acting on a runner’s leg during a stride or the forces acting on a swimmer’s arm during a stroke.
FAQ Corner
What is the significance of Newton’s Second Law?
Newton’s Second Law provides a quantitative relationship between force, mass, and acceleration, allowing us to calculate the force acting on an object based on its mass and the acceleration it experiences.
How do we convert between different units of force?
To convert between different units of force, such as Newtons, pounds, and kilograms, we use conversion factors that relate the units. For example, 1 Newton is approximately equal to 0.2248 pounds.
What are the potential sources of error when solving for t1?
Potential sources of error include incorrect measurements of mass or acceleration, as well as rounding errors during calculations. It’s important to ensure accurate measurements and use appropriate precision in calculations to minimize errors.
